はじめに
「IQが20離れると会話が成立しない」という俗説を耳にしたことがあるでしょうか。知能指数の差が大きいと、互いの理解が困難になり、コミュニケーションが円滑に進まないという主張です。この説の真偽や心理学的妥当性については様々な議論がありますが、本記事ではそうした考察には踏み込みません。
本記事の問いは極めてシンプルです。「もし『IQ差が±20以内でなければ会話が成立しない』という条件を仮定したとき、任意のIQ値を持つ人が、ランダムに選ばれた相手と会話が成立しない確率はどの程度になるのか?」という素朴な知的好奇心から出発します。
これは心理学的・社会学的な深い考察ではなく、あくまで単純なモデルを置き、確率を計算してみる思考実験です。数学的な枠組みを使って、この俗説が統計的にどのような含意を持つのかを探ってみたいと思います。
IQと正規分布の前提|問題設定
まず、計算の前提を明確にしておきます。
IQは正規分布に従うと仮定します。正規分布とは、平均値を中心に左右対称な釣鐘型の分布を描く確率分布です。一般に、平均\(\mu\)、標準偏差\(\sigma\)の正規分布を\(N(\mu, \sigma^2)\)と表記します。
IQの主流の定義に従い、平均を\(\mu = 100\)、標準偏差を\(\sigma = 15\)とします。したがって、母集団におけるIQの分布は正規分布\(N(100, 15^2)\)に従うと仮定します。IQが精神年齢/実年齢という歴史的定義から現代の統計的定義へと変遷した経緯、および平均・分散・標準偏差の詳細については、既存記事「IQスコアとは何か?知能指数を統計で読み解く|平均・標準偏差・偏差値の徹底解説」をご参照ください。また、IQの定義を偏差値の考え方と関連付けた解説については「IQと偏差値の関係|相互変換の公式と計算例を完全解説」をご参照ください。
次に、問題設定を行います。自分自身のIQを定数\(\alpha\)とします。一方、ランダムに選ばれた相手のIQを考えます。相手を選ぶ前の段階では、相手のIQはまだ決まっていない不確定な量です。このような「ランダムな状態にある量」を、数学では確率変数と呼びます。
表記の注意:本記事では、確率変数(ランダムな状態にある量)を大文字の\(X\)で表し、確率変数が実際に取る具体的な値を小文字の\(x\)で表します。例えば、「ランダムに選ばれた相手のIQ」という確率変数を\(X\)と書き、「実際に測定したら\(x = 115\)だった」という具体的な値を\(x\)で表すという使い分けです。
この相手のIQを確率変数\(X\)と表記します。確率変数がどのような値を取りやすいかを記述するものを確率分布と呼びます。\(X\)の確率分布を以下のように表記します:
$$X \sim N(100, 15^2)$$
ここで記号「\(\sim\)」は「〜に従う(follows a distribution)」という意味の統計学の標準表記です。これは近似を表す記号ではありません。この式は「確率変数\(X\)が、平均100、分散\(15^2\)の正規分布に従って値を取る」ことを意味します。言い換えれば、母集団からランダムに1人選んだとき、その人のIQは平均100、標準偏差15の正規分布に沿って分布しているということです。
「会話が成立する」という条件を、俗説に従い「IQ差が±20以内」と定義します。すなわち、
$$\alpha – 20 \le X \le \alpha + 20$$
が成り立つとき、会話が成立するとします。この条件は俗説をそのまま採用したものであり、実際の会話成立条件を正確に反映しているわけではありません。あくまでモデル上の仮定です。
正規分布の確率密度関数
確率を計算するために、正規分布の確率密度関数を導入します。
正規分布\(N(\mu, \sigma^2)\)の確率密度関数は、一般に次のように定義されます。
$$f(x) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left( -\frac{(x-\mu)^2}{2\sigma^2} \right)$$
ここで、\(\mu\)は平均、\(\sigma\)は標準偏差、\(x\)は確率変数が取りうる具体的な値を表します。今回の場合、\(x\)は相手のIQの具体的な数値(例えば100、115、130など)を意味します。
今回の設定では\(\mu = 100\)、\(\sigma = 15\)ですから、確率密度関数は次のように具体化されます。
$$f(x) = \frac{1}{\sqrt{2\pi} \cdot 15} \exp\left( -\frac{(x-100)^2}{2 \cdot 15^2} \right)$$
また、累積分布関数\(\Phi(z)\)を導入します。これは標準正規分布\(N(0,1)\)において、確率変数が\(z\)以下である確率を表す関数です。すなわち、
$$\Phi(z) = \int_{-\infty}^{z} \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{t^2}{2}\right) dt$$
と定義されます。正規分布の確率計算には、この累積分布関数が不可欠です。
なお、標準正規分布の累積分布関数は以下の重要な性質を持ちます:
$$\Phi(-z) = 1 – \Phi(z)$$
これは標準正規分布が原点対称であることから導かれる性質で、後の証明で使用します。
会話が成立する確率・成立しない確率の導出
会話が成立する確率を\(p(\alpha)\)と定義します。これは、確率変数\(X\)(相手のIQ)が\(\alpha – 20\)以上\(\alpha + 20\)以下である確率です。
$$p(\alpha) = P(\alpha – 20 \le X \le \alpha + 20) = \int_{\alpha-20}^{\alpha+20} f(x) \, dx$$
この積分を、標準正規分布の累積分布関数\(\Phi\)を用いて表現するため、変数変換を行います。
変数変換
$$t = \frac{x – 100}{15}$$
を行うと、\(X\)を標準化した確率変数
$$T = \frac{X – 100}{15}$$
は標準正規分布\(N(0, 1)\)に従います。このとき、
$$p(\alpha) = P\left(\frac{\alpha – 20 – 100}{15} \le T \le \frac{\alpha + 20 – 100}{15}\right)$$
となり、累積分布関数\(\Phi\)を用いて次のように表現できます。
$$p(\alpha) = \Phi\left(\frac{\alpha + 20 – 100}{15}\right) – \Phi\left(\frac{\alpha – 20 – 100}{15}\right)$$
整理すると、
$$p(\alpha) = \Phi\left(\frac{\alpha – 80}{15}\right) – \Phi\left(\frac{\alpha – 120}{15}\right)$$
となります。
ここで、\(\alpha – 80 = (\alpha – 100) + 20\)、\(\alpha – 120 = (\alpha – 100) – 20\)と変形できることに注目しましょう。これを代入すると:
$$p(\alpha) = \Phi\left(\frac{(\alpha – 100) + 20}{15}\right) – \Phi\left(\frac{(\alpha – 100) – 20}{15}\right)$$
この式から、\(p(\alpha)\)は\(\alpha – 100\)、すなわち平均からの偏差のみに依存し、\(\alpha = 100\)を中心に対称な関数であることがわかります。言い換えれば、\(p(100 + k) = p(100 – k)\)が任意の\(k\)について成り立ちます。
次に、会話が成立しない確率を\(q(\alpha)\)と定義します。これは\(p(\alpha)\)の補事象ですから、
$$q(\alpha) = 1 – p(\alpha)$$
すなわち、
$$q(\alpha) = 1 – \left[ \Phi\left(\frac{\alpha – 80}{15}\right) – \Phi\left(\frac{\alpha – 120}{15}\right) \right]$$
\(p(\alpha)\)が\(\alpha = 100\)を中心に対称であるため、\(q(\alpha)\)も同様に\(\alpha = 100\)を中心に対称な関数となります。つまり、\(q(100 + k) = q(100 – k)\)が成り立ちます。この対称性により、例えばIQ 130での孤立確率とIQ 70での孤立確率は等しく、IQ 160での孤立確率とIQ 40での孤立確率も等しくなります。
この\(q(\alpha)\)は、IQ値\(\alpha\)に依存する関数です。つまり、自分のIQがいくつであるかによって、会話が成立しない確率は変化します。
微分による最小値の証明
ここで、\(q(\alpha)\)が\(\alpha = 100\)で最小値をとることを微分を用いて示します。
\(q(\alpha)\)を\(\alpha\)で微分すると:
$$\frac{dq}{d\alpha} = -\frac{1}{15}\left[ f\left(\frac{\alpha – 80}{15}\right) – f\left(\frac{\alpha – 120}{15}\right) \right]$$
ここで\(f\)は標準正規分布の確率密度関数です。\(\alpha = 100\)のとき、正規分布の対称性\(f(z) = f(-z)\)から:
$$\frac{dq}{d\alpha}\Big|_{\alpha=100} = -\frac{1}{15}\left[ f\left(\frac{20}{15}\right) – f\left(\frac{-20}{15}\right) \right] = 0$$
これは\(\alpha = 100\)が\(q(\alpha)\)の停留点(変化率が0になる点)であることを示します。
次にこの点が極大・極小・変曲点のいずれであるかを判定するため、2階微分を計算します。標準正規分布の確率密度関数を\(f(z) = \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{z^2}{2}\right)\)とすると、\(f'(z) = -z \cdot f(z)\)となります。これを用いて:
$$\frac{d^2q}{d\alpha^2} = -\frac{1}{15^2}\left[ f’\left(\frac{\alpha – 80}{15}\right) – f’\left(\frac{\alpha – 120}{15}\right) \right]$$
\(\alpha = 100\)のとき:
$$\frac{d^2q}{d\alpha^2}\Big|_{\alpha=100} = -\frac{1}{225}\left[ -\frac{20}{15} f\left(\frac{20}{15}\right) -\frac{20}{15} f\left(\frac{-20}{15}\right) \right]$$
対称性\(f(z) = f(-z)\)を用いると:
$$= -\frac{1}{225}\left[ -\frac{40}{15} f\left(\frac{20}{15}\right) \right] = \frac{40}{225 \cdot 15} f\left(\frac{20}{15}\right) > 0$$
\(f(z) > 0\)なので、2階微分は正です。これは\(\alpha = 100\)の近傍で関数が下に凸(二次関数で言えば\(x^2\)の係数が正のような形)であることを示しています。したがって、\(\alpha = 100\)で最小値をとることが確認できます。
また、先ほど示した代数的な変形により、\(q(\alpha)\)は\(\alpha = 100\)を中心に左右対称な関数となることが確認できます。
\(\alpha \to \infty\)のときの極限
\(\alpha\)が無限大に発散するとき、\(q(\alpha)\)がどのような値に収束するかを調べてみましょう。
$$q(\alpha) = 1 – \left[ \Phi\left(\frac{\alpha – 80}{15}\right) – \Phi\left(\frac{\alpha – 120}{15}\right) \right]$$
累積分布関数\(\Phi(z)\)の定義より:
$$\Phi(z) = \int_{-\infty}^{z} \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{t^2}{2}\right) dt$$
\(\alpha \to \infty\)のとき、\(\frac{\alpha – 80}{15} \to \infty\)、\(\frac{\alpha – 120}{15} \to \infty\)であるから:
$$\lim_{\alpha \to \infty} \Phi\left(\frac{\alpha – 80}{15}\right) = \lim_{z \to \infty} \int_{-\infty}^{z} \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{t^2}{2}\right) dt = \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{t^2}{2}\right) dt$$
ここで、確率密度関数の全空間での積分は、確率の定義より1です。これは全事象の確率が1であることを意味します:
$$\int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{t^2}{2}\right) dt = 1$$
したがって:
$$\lim_{\alpha \to \infty} \Phi\left(\frac{\alpha – 80}{15}\right) = 1$$
同様に:
$$\lim_{\alpha \to \infty} \Phi\left(\frac{\alpha – 120}{15}\right) = 1$$
よって:
$$\lim_{\alpha \to \infty} q(\alpha) = 1 – (1 – 1) = 1$$
同様に、対称性から\(\alpha \to -\infty\)のときも\(q(\alpha) \to 1\)となります。
これは直感的にも理解できます。IQが極端に高く(または低く)なると、母集団の中で「IQ差が±20以内」という条件を満たす相手はほとんど存在しなくなるため、会話が成立しない確率は限りなく100%に近づきます。
Taylor展開による簡易モデル
ここまでの議論では厳密な式を用いてきましたが、\(\alpha\)が平均100に近い場合、Taylor展開を用いることでより簡潔な近似式を得ることができます。
\(q(\alpha)\)を\(\alpha = 100\)の周りで2次のTaylor展開を行い、3次以降の高次項(剰余項)を無視します。1階微分が0であることから、2次の項までで:
$$q(\alpha) \approx q(100) + \frac{1}{2}\frac{d^2q}{d\alpha^2}\Big|_{\alpha=100} (\alpha – 100)^2$$
先ほど計算した2階微分の値を用いると:
$$q(\alpha) \approx 0.183 + \frac{40}{225 \cdot 15} f\left(\frac{20}{15}\right) \cdot \frac{(\alpha – 100)^2}{2}$$
ここで\(f\left(\frac{20}{15}\right) = f(1.33) \approx 0.164\)なので:
$$q(\alpha) \approx 0.183 + 0.0019 \cdot (\alpha – 100)^2$$
この近似式から、会話が成立しない確率は\(\alpha = 100\)からの距離の2乗に比例して増加することがわかります。つまり、平均から10離れるよりも、20離れる方が4倍速く孤立確率が増加するのです。
ただし、この近似は\(\alpha\)が100から大きく離れると精度が落ちるため、あくまで定性的な理解のためのモデルとして捉えてください。
IQ別の会話成立確率|数値例とグラフで可視化
ここで、具体的な数値を代入して\(q(\alpha)\)の値を確認してみましょう。
\(\alpha = 100\)(平均)のとき:
$$q(100) = 1 – \left[ \Phi\left(\frac{20}{15}\right) – \Phi\left(\frac{-20}{15}\right) \right] \approx 0.183$$
つまり約18.3%です。平均的なIQを持つ人でも、ランダムに選ばれた相手と会話が成立しない確率は約2割弱あるということです。
- \(\alpha = 115\)のとき:\(q(115) \approx 0.38\)
すなわち約38%です。 - \(\alpha = 130\)のとき:\(q(130) \approx 0.748\)
すなわち約75%にもなります。
下のグラフは、IQ値\(\alpha\)と会話が成立しない確率\(q(\alpha)\)の関係を示したものです。青い実線が厳密な計算による曲線、オレンジの破線はTaylor展開による近似曲線です。
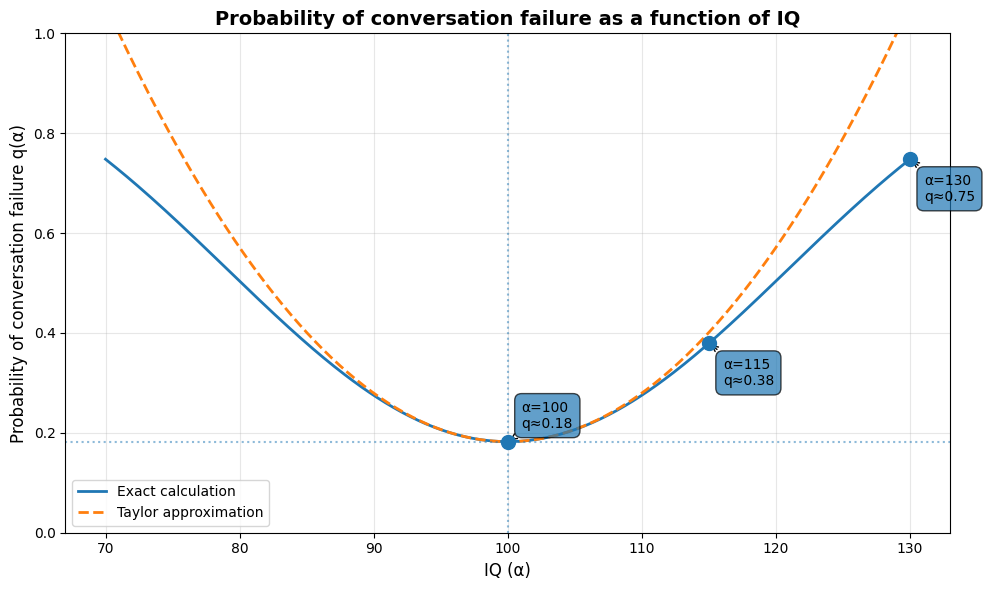
青い実線は正規分布モデルによる厳密な計算結果、オレンジの破線はTaylor展開による2次近似。IQ 100で最小値(18.3%)を取り、平均から離れるほど左右対称に確率が増加する。
グラフから、\(\alpha = 100\)で最小値をとり、平均から離れるほど左右対称に確率が増加することが視覚的に確認できます。この対称性は、先ほど示した\(\alpha – 80 = (\alpha – 100) + 20\)、\(\alpha – 120 = (\alpha – 100) – 20\)という変形から数式的に保証されています。Taylor近似は\(\alpha = 100\)付近では厳密な値とよく一致していますが、\(\alpha\)が100から離れるにつれて乖離が大きくなることもわかります。
次のグラフは、IQ 100から200までの範囲での\(q(\alpha)\)の振る舞いを示しています。
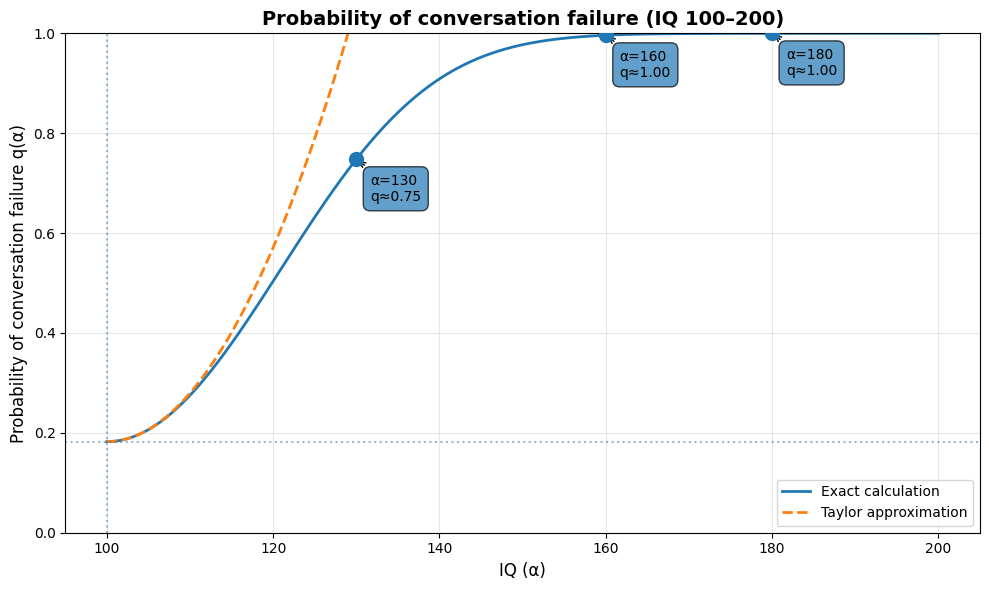
IQが平均から大きく離れると孤立確率は急激に上昇し、IQ 160以上ではほぼ100%に収束する。対称性により、低IQ側でも同様の傾向を示す(IQ 40 ≈ IQ 160の孤立確率)。
IQ 160以上では会話が成立しない確率がほぼ100%(\(q \approx 1.00\))に達することがわかります。先ほど示した代数的変形により、IQ 100より左側(低IQ側)の振る舞いは、右側を100を中心に反転させたものと同じになります。つまり、IQ 70での孤立確率(約75%)はIQ 130と同程度、IQ 40での孤立確率はIQ 160と同程度(ほぼ100%)になります。
極端な値での確率を示すと:
- \(\alpha = 160\)のとき:\(q(160) \approx 0.9999659722\)(約99.997%、会話が成立する確率は約\(3.40 \times 10^{-5}\)、すなわち約0.003%)
- \(\alpha = 180\)のとき:\(q(180) \approx 0.9999999987\)(約99.99999999%、会話が成立する確率は約\(1.28 \times 10^{-9}\)、すなわち約0.000000128%)
- \(\alpha = 200\)のとき:\(q(200) \approx 1.0000000000\)(実質的に100%、会話が成立する確率は約\(6.22 \times 10^{-15}\))
ただし、ここで注意が必要です。WAIS(ウェクスラー成人知能検査)など主要なIQ検査における測定上限は160程度です。したがって、IQ 160を超える値は、通常の心理検査では測定できません。IQ 180やIQ 200といった値は、ハイレンジIQテストにおいて統計的に算出される値であり、標準的なIQ検査の範囲を超えています。本記事のモデルはあくまで正規分布を仮定した数学的な思考実験であり、これらの極端な値は理論上の計算結果として捉えてください。
このように、IQが平均から大きく離れると、会話が成立しない確率は実質的に1(100%)に収束します。
結果の解釈と注意点
これまでの計算から、いくつかの重要な知見が得られました。ここでは、この結果が持つ含意について考察します。
まず、これは能力の優劣を示すものではありません。あくまで母集団分布との重なりの問題です。平均から離れたIQを持つ人は、単純に「自分と±20以内のIQを持つ人」が母集団の中に少ないため、統計的に会話相手を見つけにくいということです。
私見を述べるならば、この結果は3つの興味深い含意を持っています。
第一に、平均にとどまることの皮肉です。\(q(\alpha)\)が\(\alpha = 100\)で最小になるということは、統計的には「平均的であること」が最も会話相手を見つけやすいことを意味します。能力的に突出することを目指す人にとって、これは皮肉な結果かもしれません。平均にとどまることが、コミュニケーションの観点からは最も有利な位置なのです。
第二に、突出することは孤立することを意味するという点です。\(\alpha\)が平均から上方向に離れるほど、\(q(\alpha)\)は増加します。高IQを持つことは、統計的にはコミュニケーション可能な相手の減少を意味します。もしあなたがIQを高めることを目指すなら、この統計的孤立を覚悟すべきでしょう。これは脅しではなく、単なる数学的帰結です。突出した能力を持つことは、それに見合う孤独を受け入れることでもあります。
第三に、下方向への孤立と社会的支援の重要性です。\(\alpha\)が平均から下方向に離れる場合も、\(q(\alpha)\)は同様に増加します。つまり、知的能力が平均より著しく低い人も、統計的には孤立しやすいということです。ただし、後見人や支援者が存在すれば状況は異なります。このモデルが示唆するのは、社会的支援が行き届かない場合の統計的孤立のリスクです。平均以下のIQを持つ人々には、適切な支援体制が不可欠であることを、このモデルは間接的に示しています。
もちろん、これらはあくまでこの単純化されたモデルが示唆することであり、個人の価値や人間関係の質を決定するものではありません。実際の会話成立には、性格、経験、興味、言語化能力、共感力など、IQ以外の多くの要因が関わります。また、「IQ差±20以内」という条件自体が俗説であり、科学的に検証されたものではありません。
まとめ
本記事では、「IQが20離れると会話が成立しない」という俗説を前提に、単純な確率モデルを用いて「会話が成立しない確率」を計算しました。
その結果、会話が成立しない確率\(q(\alpha)\)はIQ値\(\alpha\)の関数であり、\(\alpha = 100\)で最小、平均から離れるほど左右対称に増加することが示されました。微分を用いた厳密な証明により、\(\alpha = 100\)が確かに最小値であることを確認しました。また、Taylor展開による簡易モデルから、孤立確率は平均からの距離の2乗に比例して増加することがわかりました。さらに、\(\alpha \to \infty\)のとき\(q(\alpha) \to 1\)となることを、確率の定義と累積分布関数の性質から示しました。
これは統計的な母集団分布との重なりの問題であり、能力の優劣を示すものではありません。しかし同時に、この結果は興味深い含意を持ちます。特に「平均にとどまることの皮肉」──すなわち、統計的には平均的であることが最も会話相手を見つけやすく、能力的に突出することは孤立のリスクを高めるという逆説的な結論は、能力向上を目指す人々にとって考えさせられる示唆と言えるでしょう。同時に、平均から下方向に離れた場合の孤立と社会的支援の必要性も、このモデルは示しています。
本記事はあくまで知的好奇心を満たすための思考実験です。この結果を現実にそのまま適用すべきではありません。IQと会話成立の関係についてのより深い考察は、必要があれば別記事で改めて扱いたいと思います。
免責事項
本記事は、IQが正規分布に従うこと、および会話成立条件を「IQ差±20以内」とする単純化されたモデルに基づく思考実験です。実際の会話成立には、性格、経験、興味、言語化能力など多くの要因が関わり、本記事のモデルが現実をそのまま反映しているわけではありません。
本記事は医学的、心理学的、社会学的助言を提供するものではありません。あくまで数学的モデルによる確率計算の一例としてお読みください。本記事の内容を実生活に適用する際は、ご自身の責任においてご判断ください。




コメント