序章：IQという数値をどう理解するか
知能を表す指標として広く知られているのがIQ（Intelligence Quotient、知能指数）です。多くの人は「IQが高いほど頭がいい」と直感的に理解していますが、ではその数値はどのように算出されているのでしょうか。意外にも、この問いに正確に答えられる人は少ないのではないでしょうか。
本記事では、IQの成り立ちを歴史的背景から振り返り、現在の統計的な測り方に至るまでの流れを整理します。さらに後半では、平均・分散・標準偏差といった統計学の基本概念を用いながら、誰でも理解できる形でIQの仕組みを解説していきます。
歴史的背景：IQという概念の変遷
昔の測り方 ― 精神年齢にもとづくIQ
20世紀初頭、フランスの心理学者ビネー（Alfred Binet）とジモン（Théodore Simon）は、子どもの学習支援のために知能検査を開発しました。ここでは精神年齢（mental age）という概念が導入され、実年齢に対してどれだけ進んでいるかを数値化する方式がとられました。たとえば8歳の子どもが10歳相当の問題に答えられると、精神年齢は10歳とされ、次のように計算されます。
\text{IQ} = \frac{\text{精神年齢}}{\text{実年齢}} \times 100
\]
この場合、IQは125となり、「年齢以上に発達している」と判断されました。
その限界 ― 成人に適用できない理由
精神年齢方式は子どもに対しては有効でしたが、成人にそのまま適用すると問題が生じます。たとえば60歳の人が30歳相当の能力を持っていると仮定すると、次のようになります。
\text{IQ} = \frac{30}{60} \times 100 = 50
\]
一見すると「年齢が高いにもかかわらず若年期と同等の能力を維持している」と評価されるべき場面でも、この方式では比率の性質により数値が過度に低く見積もられます。すなわち、成人に精神年齢方式を単純適用するのは不適切であり、別の定義が必要になるのです。
現在の測り方 ― 統計的にもとづくIQ
この欠点を解決するために導入されたのが、統計的基準にもとづくIQです。代表例がWAIS（ウェクスラー成人知能検査）で、集団全体の平均を100、標準偏差を15と設定し、各個人の得点が「平均からどれくらい離れているか」を数値化します。これにより、成人を含むあらゆる年齢層で相対的に妥当な測定が可能になりました。
ここで出てくる平均や標準偏差といった統計用語は難しく感じるかもしれませんが、次の章で具体例を使いながらわかりやすく解説します。まずは「IQは精神年齢方式から統計方式へと移行した」という流れを押さえてください。
平均・分散・標準偏差とは何か？
ここからは、IQスコアを理解するうえで欠かせない3つの統計的な概念 ― 平均・分散・標準偏差 ― を解説します。まず平均、次に分散、最後に標準偏差の順に説明します。
平均（Mean）とは何か？
まずは最も基本となる「平均」から確認しましょう。平均とは、すべての値を合計して、その個数で割ったものです。これは学校のテストや日常生活でも頻繁に使う考え方です。
すべての点数を合計し人数で割ると平均値が得られます
例1： 3人のテスト点数が 60点・70点・80点 の場合。
- 合計：60 + 70 + 80 = 210
- 人数：3人
- 平均：210 ÷ 3 = 70
つまり、このクラスの平均点は70点です。これは「全員の点数を集めて、平等に分けたら1人あたり何点になるか」を表しています。
例2： 1週間の睡眠時間を考えてみましょう。月曜6時間、火曜7時間、水曜5時間、木曜8時間、金曜6時間、土曜7時間、日曜9時間とします。
- 合計：6 + 7 + 5 + 8 + 6 + 7 + 9 = 48
- 日数：7日
- 平均：48 ÷ 7 ≈ 6.86時間
この場合の平均睡眠時間は約6.9時間となります。つまり「毎日同じだけ寝ていたら1日あたりどのくらいか」を示す値です。
分散（Variance）
分散とは「データが平均からどれだけ離れているか」を測る指標です。ただズレをそのまま足すと正負が打ち消し合ってしまうので、ズレを二乗して足し合わせます。
二乗を用いる発想は三平方の定理と同じ。距離や広がりを自然に測る仕組みです
この二乗という操作を直感的に理解するために、三平方の定理を使ってみましょう。直角三角形の辺の長さを \(a, b, c\) とするとき、
a^2 + b^2 = c^2
\]
となります。
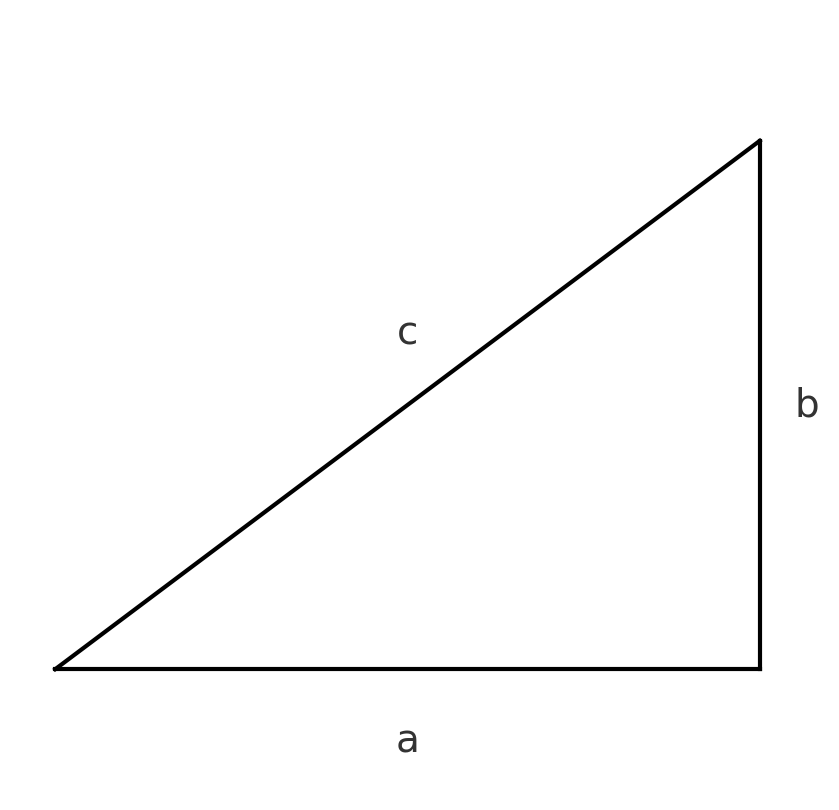
三平方の定理：斜辺の二乗は他の辺の二乗の和に等しい
「斜辺 \(c\) の長さの二乗を求めるには、残りの辺 \(a, b\) の二乗を足せばよい」という考え方です。分散も同じで、「平均からの差」を二乗して足すことで、全体のズレの大きさを測っています。二点間の距離を二乗して足すのと同じ感覚で、自然な操作なのです。
この類推は3次元以上にも広げられます。例えば点が3つある場合も、2回三平方の定理を使えば距離が求められます。一般に「次元」とはざっくり言えば座標軸の本数のことです（※正確には基底の数ですが、ここでは直感的な説明にとどめます）。
平均が同じで分散が違うデータセットの比較
ここでは、平均値は同じなのに分散が異なる2つのデータセットを考えてみます。数値がどのように散らばっているかを体感できる例です。
平均が同じでも分散の大きさによってデータの散らばり方は変わります
データセットA（平らな分布）
| 点数 | 人数 |
|---|---|
| 60 | 5 |
| 65 | 5 |
| 70 | 5 |
| 75 | 5 |
| 80 | 5 |
平均値は70点です。次に分散を計算してみましょう。
\frac{(60-70)^2 \times 5 + (65-70)^2 \times 5 + (70-70)^2 \times 5 + (75-70)^2 \times 5 + (80-70)^2 \times 5}{25}
= 50
\]
データセットB（中央に集中）
| 点数 | 人数 |
|---|---|
| 60 | 1 |
| 65 | 4 |
| 70 | 10 |
| 75 | 4 |
| 80 | 1 |
こちらも平均値は70点です。分散を計算してみると──
\frac{(60-70)^2 \times 1 + (65-70)^2 \times 4 + (70-70)^2 \times 10 + (75-70)^2 \times 4 + (80-70)^2 \times 1}{20}
= 20
\]
結果の比較
両方のデータは「平均70」で同じ中心値を持っています。しかし分散はAが50、Bが20となり、Bのほうが値が平均に集中していることが分かります。つまり、分散は「広がり具合」を数値で表す指標なのです。
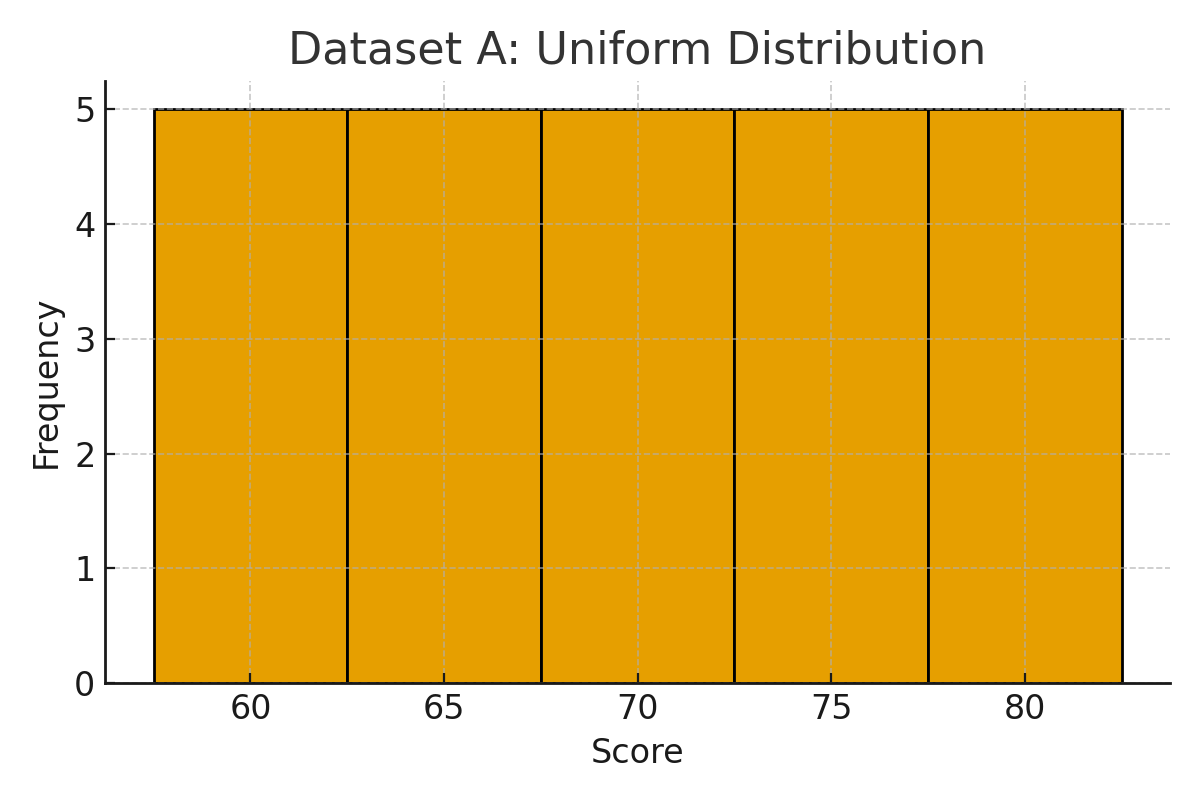
データセットA：平らに広がる分布（分散が大きい）
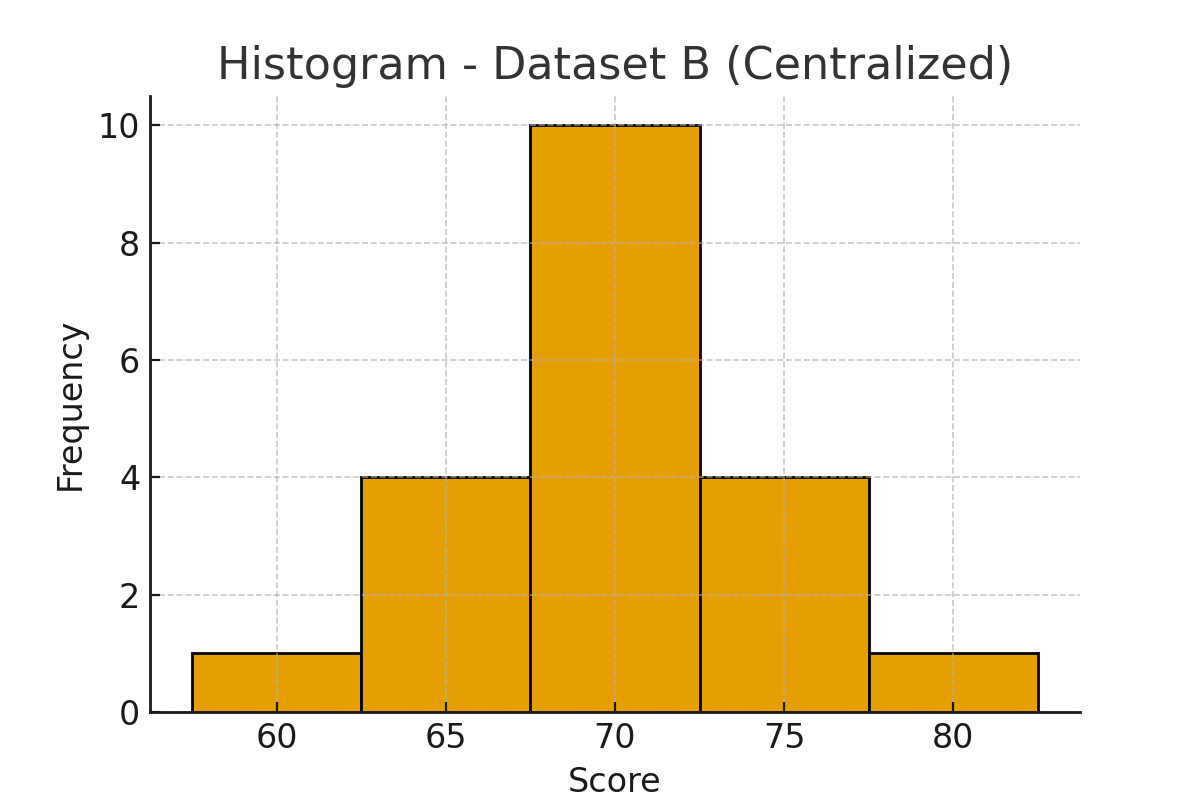
データセットB：中央に集中する分布（分散が小さい）
すぐ試せる一歩：自分の最近のテスト点（または睡眠時間・歩数）を5〜7件だけメモし、平均→各値との差→差の二乗を合計→件数で割る（分散）をやってみましょう。A/Bのヒストグラムと見比べて、広がりの感覚を言葉で説明してみると理解が定着します。
標準偏差（Standard Deviation）
標準偏差は、分散の平方根です。分散は「平均からのズレの二乗の平均」でしたが、二乗したままだと単位がズレます。そこで最後に平方根をとると、もとの尺度（点数や時間など）に戻せます。これは三平方の定理で \(a^2+b^2=c^2\) から、最後に \(c=\sqrt{a^2+b^2}\) と“長さ”を取り出すのと同じ発想です。
直感的には、「平均からどれくらい離れているか」を“距離”として表す指標が標準偏差です。値が小さいほど平均の近くに集まり、大きいほど広く散らばっています。
今回の2つのデータセットでの標準偏差（母分散基準）
\text{Aの分散}=50 \;\Rightarrow\; \text{Aの標準偏差}=\sqrt{50}\approx 7.07
\]
\text{Bの分散}=20 \;\Rightarrow\; \text{Bの標準偏差}=\sqrt{20}\approx 4.47
\]
すぐ試せる一歩：上で出した分散値に電卓で平方根を適用し、標準偏差を算出してみましょう。自分のデータで「集中している／広がっている」の実感が得られます。
統計記号の導入：ギリシャ文字で一般式を書く
ここまで具体例で平均・分散・標準偏差を見てきました。次に、それらを数式で表現するために使われる記号を紹介します。初めて見ると難しく感じるかもしれませんが、意味を押さえればシンプルです。
総和記号（シグマ, Σ）
Σ（シグマ）は「合計」を意味する記号です。英語の SUM の頭文字Sに対応しており、「すべて足し合わせる」という操作を表します。
\sum_{i=1}^{n} X_i = X_1 + X_2 + X_3 + \cdots + X_n
\]
「\(X_i\)」はデータの一つひとつを指し、\(i\) は番号を表しています。つまり「1番目からn番目までの値を合計する」という意味になります。
平均（Mean, μ）
平均は「全ての値を合計して、データの個数で割ったもの」です。これを数式にすると次のようになります。
\mu = \frac{1}{n} \sum_{i=1}^{n} X_i
\]
ここで μ（ミュー）は「平均」を表す記号で、英単語 mean の頭文字「m」に由来します。
分散（Variance, σ²）
分散は「各データが平均からどれだけ離れているか」を二乗して合計し、全体で割ったものです。
\sigma^2 = \frac{1}{n} \sum_{i=1}^{n} (X_i – \mu)^2
\]
標準偏差（Standard Deviation, σ）
標準偏差は分散の平方根で、次のように表されます。
\sigma = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (X_i – \mu)^2}
\]
平方根を取るのは、三平方の定理で最後に斜辺の長さを求めるのと同じで、「二乗した数」をもとに“距離”を取り出すためです。
まとめと次回予告
ここまで、IQを理解するための基礎として「平均」「分散」「標準偏差」を具体例と数式を交えて解説しました。統計学的な視点を持つことで、IQという数値が単なる「頭の良さ」ではなく、集団の中での位置づけを表す指標であることが見えてきます。
次回は、この基礎を踏まえて「偏差値とIQの関係」について詳しく解説します。なぜIQ100が「平均」とされるのか、そしてIQ130が「上位2%」と言われる根拠はどこから来ているのか──その構造を数式と具体例を通して明らかにしていきます。
著者について
本記事は、IQや認知科学の研究と実践を重ねる筆者の視点から執筆されています。
「天才は後天的に育てられる」という信念を軸に、誰もが日常の中で知性を鍛えられる方法を探究しています。
筆者のプロフィールや本ブログ全体の理念については、運営者情報ページをご覧ください。
ご質問やご感想などがあれば、運営者情報ページに記載されているメールアドレスへお気軽にお寄せください。
コメント