序章:上位2%とはどれだけすごいのか
「上位2%」と聞いて、どれほど特別なことなのかすぐにイメージできる人は少ないと思います。日常生活では「トップ3に入った」「100点満点だった」という分かりやすい基準で成果を測ることが多いため、割合で示される「上位○%」という表現はピンと来ないのです。そこで今回は、この「上位2%」が持つ統計的な意味を、できるだけシンプルに解説していきます。
シンプルな例で考えてみる
まずは小さな例から始めましょう。100人が同じテストを受けたとします。上位2%というのは「100人のうち上から2人」に入るということです。500人なら10人、1000人なら20人。ここまでは単純に「全体人数 × 割合」で求めることができます。
この段階では直感的に理解できるはずです。「上位2%」とは全体を並べたときの一番上から数えて、その割合にあたる人数を切り出すことを意味します。
まとめとアクション
- 上位数%は「全体人数 × 割合」でまず理解できる
- シンプルに「人数」でイメージするのが第一歩
データが多すぎるときに出てくる問題
ところが、対象が数万人・数十万人に広がるとどうでしょうか。すべての点数を並べ替えて「上から2%」を探すのは、現実的に不可能です。
このとき活躍するのが「曲線として分布をみなす」という考え方です。人数が増えれば増えるほど、点の集合はなめらかな形に近づいていきます。そのため、グラフ全体を曲線で近似し、その曲線をどこで区切れば右側が全体の2%になるかを考えればよいのです。
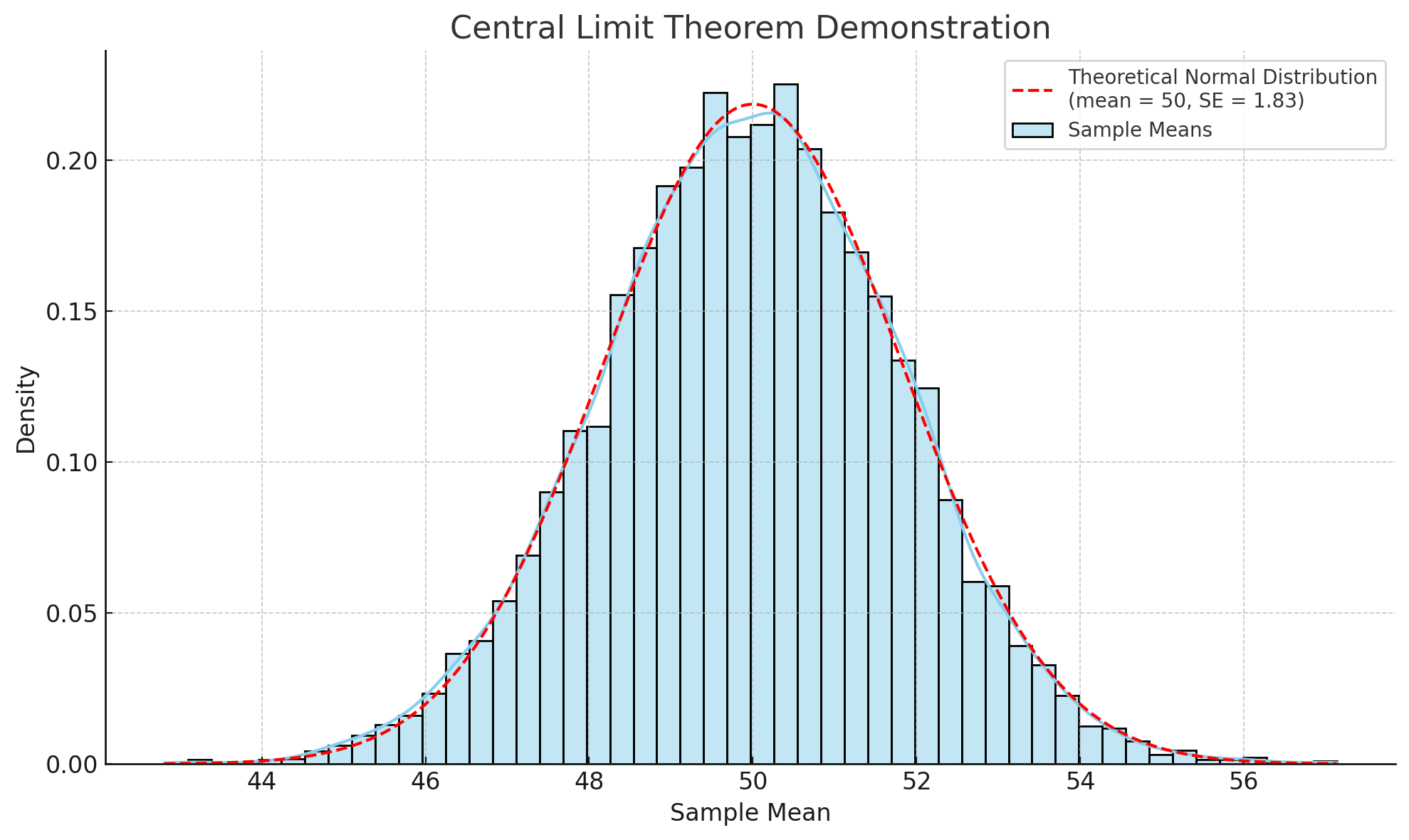
まとめとアクション
- 人数が多すぎると並べ替えは困難
- 曲線として「面積比」で考えると便利
上位2%を求める仕組み
では、曲線のどこから右側を切り取れば全体の2%になるのでしょうか。ここで使われるのが zスコア です。
定義は次の式で表されます:
- \(X\):ある人の得点
- \(\mu\):平均値(参考:平均・分散・標準偏差の解説)
- \(\sigma\):標準偏差
まとめとアクション
- zスコアは「平均からの離れ具合」を示す数値
- 平均や標準偏差の計算方法は過去記事を参照
zスコア表の見方
zスコアの値そのものを使うには「表」を見る必要があります。表には「ある点までの累積割合」が掲載されています。
今回の目的は「上位2%」です。右側が0.02になるので、左側は0.98です。表の中から「0.02に近い数値」を探すと 0.0202 が見つかります。これに対応する \(z\) の値は 2.05 です。
つまり「平均より標準偏差2倍ちょっと上の点」から右側を切り取ると、その面積が全体の2%になるのです。
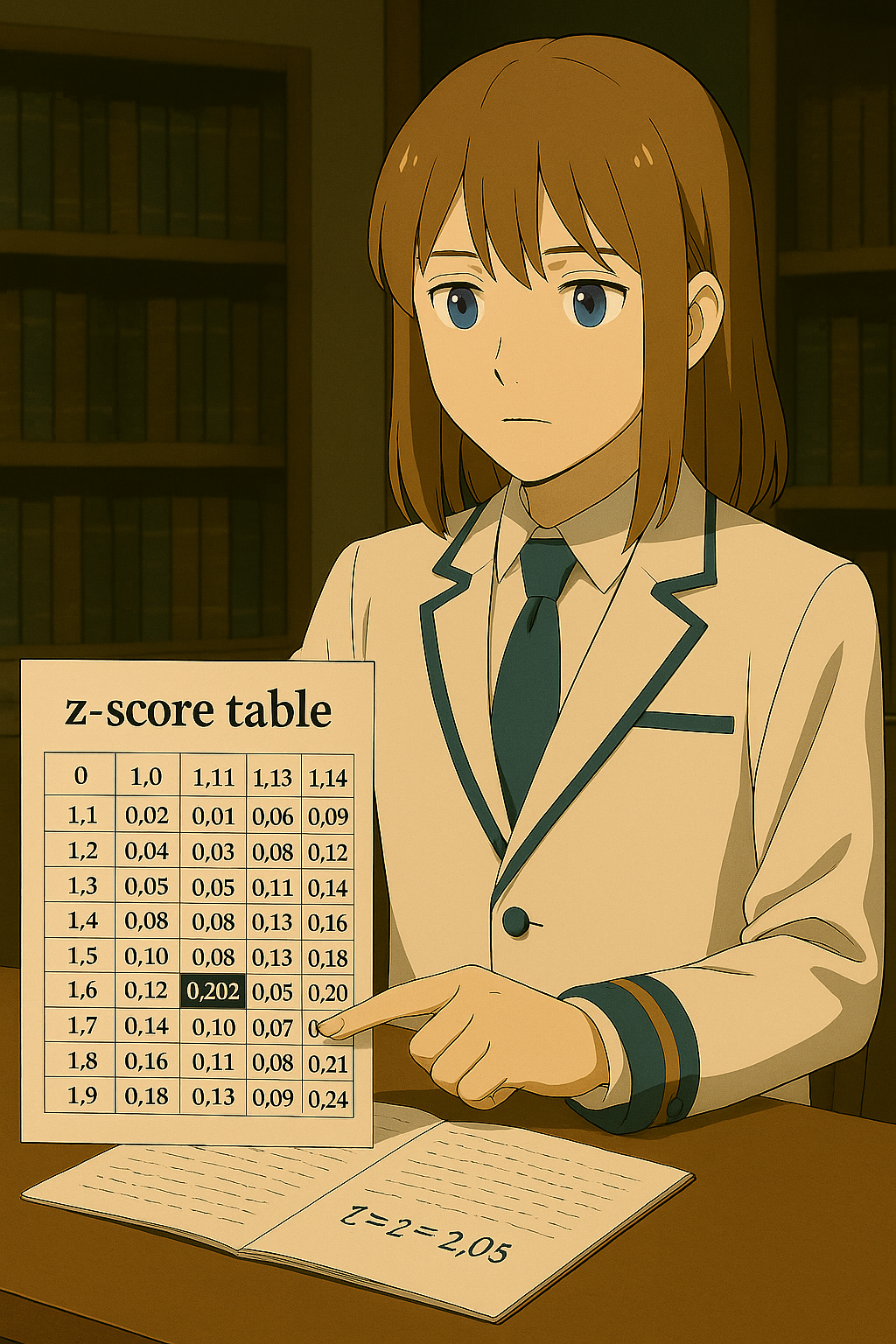
Zスコア表から0.02に近い数値を探して読み取る様子
まとめとアクション
- 上位2%は \(z \approx 2.05\) で決まる
- 表の見方は「割合を探して、行と列から\(z\)を読む」
実際にIQで計算してみる
ここでIQを例に考えてみます。IQの定義は「平均=100」です。今回は「標準偏差=15」とします。

「X = μ + zσ」の計算式を使ってIQ131を導く場面
つまり「IQ131以上」が、ちょうど上位2%のラインとなります。

累積曲線上で上位2%に対応するIQ131を示す場面
別の例:上位20%の境界点
次に、以前の記事で扱ったテストの例を再利用します。平均70点、標準偏差約13.96のテストで「上位20%」を求めます。
上位20%は右側が0.20なので、左側は0.80。表を見ると \(z \approx 0.84\) です。
つまり 82点以上 が上位20%の目安となります。
実際のサンプルデータでは95点や85点の人が上位20%に含まれていました。ただし人数が少ないと誤差が出やすく、大きな集団で見るほど安定した結果になります。
まとめとアクション
- 上位数%は「zスコア表 → 計算」で導ける
- 少人数だとズレやすいので注意
警鐘:標準偏差を明示しない危険性
最後に重要な注意点を述べます。同じ「上位2%」でも、標準偏差が違うと得点は大きく変わります。
- 標準偏差=15 の場合:\(100 + (2.05 \times 15) \approx 131\)
- 標準偏差=50 の場合:\(100 + (2.05 \times 50) \approx 203\)
つまり IQ131 と IQ203 が、どちらも「上位2%」を表してしまうのです。
もし標準偏差を隠して「IQ200」と言っても、数字だけ見れば間違いではありません。しかし、読み手は「何を基準に200なのか」を理解できず、誤解を招いてしまいます。だからこそ、IQを語るときには必ず標準偏差を併記することが欠かせません。
まとめとアクション
- IQは「数値+標準偏差」のセットで解釈すべき
- 併記しないと意味が変質してしまう
まとめ
上位2%は「全体の中でどれだけ上か」を示す割合であり、人数が多いときには曲線として分布を近似して面積比で考える必要があります。実際に計算すると、上位2%は \(z=2.05 \)に相当し、標準偏差15のIQ尺度では131がその境界となります。また、上位20%も同じ手法で求められ、例として82点以上がその基準になることがわかります。しかし、標準偏差を変えると数値は大きく変動し、標準偏差50では上位2%がIQ203に相当してしまいます。このことから、IQを論じる際には必ず標準偏差を併記しなければならないのです。




コメント